Veljko Milkovic invented a mechanical device which outputs more work than it takes to run it.
It is so simple to build that there are many replications all over the world and it is spreading fast - for the last several years.
This is yet another device, which defeats the equal and opposite reaction requirement - similar to the Fernando Sixto Ramos Solano Force Multiplier. The reaction in this machine helps to produce work in the forward direction instead of countering the input. It's mechanical jujitsu.
There is a new website they put together - Welcome to the World of Pendulum Power - Veljko Milkovic's Two-Stage Mechanical Oscillator - Official presentation
The old site is still there: Veljko Milkovic - Home Page - Official presentation of the researcher and inventor Veljko Milkovic
--------------------------------------------------------------------------------------------------------------
Mechanical Oscillator - The Pendulum-Lever System
- A Mechanical Amplifier of Clean Energy -
Free Mechanical Energy Device
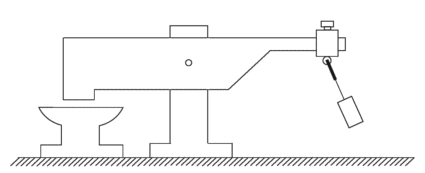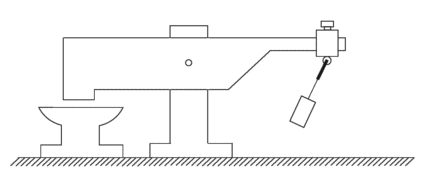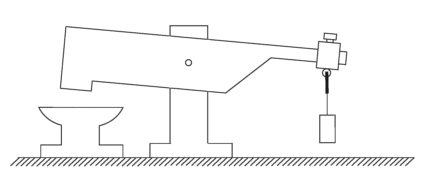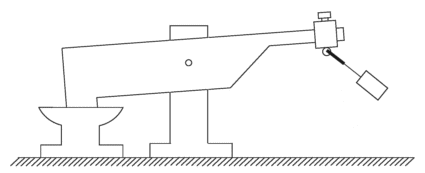 A simple mechanism with new mechanical effects, represents the source of clean mechanical energy. This gravity machine has only two main parts: a massive lever and a pendulum. The interaction of the two-stage lever multiplies input energy into output energy convenient for useful work (mechanical hammer, press, pump, transmission, electric generator...).
A simple mechanism with new mechanical effects, represents the source of clean mechanical energy. This gravity machine has only two main parts: a massive lever and a pendulum. The interaction of the two-stage lever multiplies input energy into output energy convenient for useful work (mechanical hammer, press, pump, transmission, electric generator...).
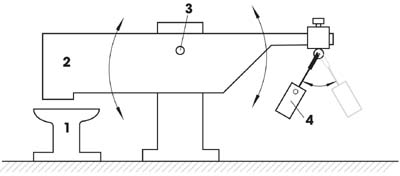
Mechanical hammer with a pendulum
1 - anvil, 2 - massive lever, 3 - lever axel, 4 - physical pendulum
The creator, inventor and constructor of the two-stage mechanical oscillator and the author of the related patents is academician Veljko Milkovic -- a Serbian internationally awarded researcher and inventor being interested in past events, ecological innovations and new clean technologies. During his successful research career, he created around 114 inventions and got 29 granted patents some of which have been in use for years.
It is so simple to build that there are many replications all over the world and it is spreading fast - for the last several years.
This is yet another device, which defeats the equal and opposite reaction requirement - similar to the Fernando Sixto Ramos Solano Force Multiplier. The reaction in this machine helps to produce work in the forward direction instead of countering the input. It's mechanical jujitsu.
There is a new website they put together - Welcome to the World of Pendulum Power - Veljko Milkovic's Two-Stage Mechanical Oscillator - Official presentation
The old site is still there: Veljko Milkovic - Home Page - Official presentation of the researcher and inventor Veljko Milkovic
--------------------------------------------------------------------------------------------------------------
Mechanical Oscillator - The Pendulum-Lever System
- A Mechanical Amplifier of Clean Energy -
Free Mechanical Energy Device


Mechanical hammer with a pendulum
1 - anvil, 2 - massive lever, 3 - lever axel, 4 - physical pendulum



Comment